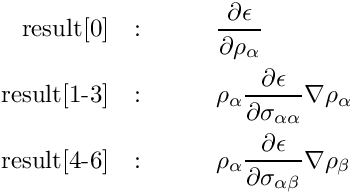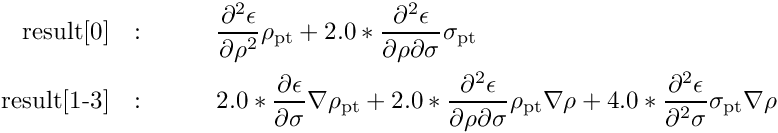Simplified interface to XC functionals. More...
#include <xcfunctional.h>
Public Types | |
| enum | xc_arg { enum_rhoa =0 , enum_rhob =1 , enum_rho_pt =2 , enum_saa =10 , enum_sab =11 , enum_sbb =12 , enum_sigtot =13 , enum_sigma_pta_div_rho =14 , enum_sigma_ptb_div_rho =15 , enum_zetaa_x =16 , enum_zetaa_y =17 , enum_zetaa_z =18 , enum_zetab_x =19 , enum_zetab_y =20 , enum_zetab_z =21 , enum_chi_aa =22 , enum_chi_ab =23 , enum_chi_bb =24 , enum_ddens_ptx =25 , enum_ddens_pty =26 , enum_ddens_ptz =27 } |
Public Member Functions | |
| XCfunctional () | |
| Default constructor is required. | |
| ~XCfunctional () | |
| Destructor. | |
| madness::Tensor< double > | exc (const std::vector< madness::Tensor< double > > &t) const |
| Computes the energy functional at given points. | |
| std::vector< madness::Tensor< double > > | fxc_apply (const std::vector< madness::Tensor< double > > &t, const int ispin) const |
| compute the second derivative of the XC energy wrt the density and apply | |
| double | get_ggatol () const |
| return the binary munging threshold for the final result in the GGA potential/kernel | |
| double | get_rhotol () const |
| return the munging threshold for the density | |
| bool | has_fxc () const |
| Returns true if the second derivative of the functional is available (not yet supported) | |
| bool | has_kxc () const |
| Returns true if the third derivative of the functional is available (not yet supported) | |
| double | hf_exchange_coefficient () const |
| Returns the value of the hf exact exchange coefficient. | |
| void | initialize (const std::string &input_line, bool polarized, World &world, const bool verbose=false) |
| Initialize the object from the user input data. | |
| bool | is_dft () const |
| Returns true if there is a DFT functional (false probably means Hatree-Fock exchange only) | |
| bool | is_gga () const |
| Returns true if the potential is gga (needs first derivatives) | |
| bool | is_lda () const |
| Returns true if the potential is lda. | |
| bool | is_meta () const |
| Returns true if the potential is meta gga (needs second derivatives ... not yet supported) | |
| bool | is_spin_polarized () const |
| Returns true if the functional is spin_polarized. | |
| void | plot () const |
| Crude function to plot the energy and potential functionals. | |
| std::vector< madness::Tensor< double > > | vxc (const std::vector< madness::Tensor< double > > &t, const int ispin) const |
| Computes components of the potential (derivative of the energy functional) at np points. | |
Static Public Member Functions | |
| static double | munge_old (double rho) |
Static Public Attributes | |
| static const int | number_xc_args =28 |
| max number of intermediates | |
Protected Member Functions | |
| void | make_libxc_args (const std::vector< madness::Tensor< double > > &t, madness::Tensor< double > &rho, madness::Tensor< double > &sigma, madness::Tensor< double > &rho_pt, madness::Tensor< double > &sigma_pt, std::vector< madness::Tensor< double > > &drho, std::vector< madness::Tensor< double > > &drho_pt, const bool need_response) const |
| convert the raw density (gradient) data to be used by the xc operators | |
Static Protected Member Functions | |
| static void | polyn (const double x, double &p, double &dpdx) |
| Smoothly switches between constant (x<xmin) and linear function (x>xmax) | |
Protected Attributes | |
| double | ggatol |
| See initialize and munge*. | |
| double | hf_coeff |
| Factor multiplying HF exchange (+1.0 gives HF) | |
| int | nderiv |
| the number of xc kernel derivatives (lda: 0, gga: 1, etc) | |
| double | rhomin |
| double | rhotol |
| See initialize and munge*. | |
| bool | spin_polarized |
| True if the functional is spin polarized. | |
Private Member Functions | |
| double | binary_munge (double rho, double refrho, const double thresh) const |
| munge rho if refrho is small | |
| double | munge (double rho) const |
| simple munging for the density only (LDA) | |
Detailed Description
Simplified interface to XC functionals.
Member Enumeration Documentation
◆ xc_arg
The ordering of the intermediates is fixed, but the code can handle non-initialized functions, so if e.g. no GGA is requested, all the corresponding vector components may be left empty.
Note the additional quantities 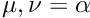
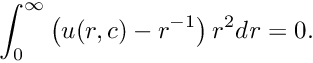
![\[
\rho = \exp(\zeta)
\]](form_352.png)
and thus the derivative of rho is given by
![\[
\nabla_x\rho = \exp(\zeta)\nabla_x\zeta = \rho \nabla_x\zeta
\]](form_353.png)
The reduced gradients \sigma may then be expressed as
![\[
\sigma = |\nabla\rho|^2 = |\rho|^2 |\nabla\zeta|^2 = |\rho|^2 \chi
\]](form_354.png)
Constructor & Destructor Documentation
◆ XCfunctional()
| madness::XCfunctional::XCfunctional | ( | ) |
◆ ~XCfunctional()
| madness::XCfunctional::~XCfunctional | ( | ) |
Destructor.
Member Function Documentation
◆ binary_munge()
|
inlineprivate |
munge rho if refrho is small
special case for perturbed densities, which might be negative and diffuse. Munge rho (e.g. the perturbed density) if the reference density refrho e.g. the ground state density is small. Only where the reference density is large enough DFT is numerically well-defined.
- Parameters
-
[in] rho number to be munged [in] refrho reference value for munging [in] thresh threshold for munging
◆ exc()
| madness::Tensor< double > madness::XCfunctional::exc | ( | const std::vector< madness::Tensor< double > > & | t | ) | const |
Computes the energy functional at given points.
This uses the convention that the total energy is ![$ E[\rho] = \int \epsilon[\rho(x)] dx$](form_361.png)
t are interpreted similarly to the xc_arg enum.
- Parameters
-
[in] t The input densities and derivatives as required by the functional
- Returns
- The exchange-correlation energy functional
References madness::c_rks_vwn5__(), madness::c_uks_vwn5__(), madness::f, std::isnan(), MADNESS_PRAGMA_CLANG, munge(), madness::pop(), madness::print(), madness::Tensor< T >::ptr(), madness::BaseTensor::size(), spin_polarized, v, madness::x_rks_s__(), madness::x_uks_s__(), and madness::xf().
Referenced by madness::xc_functional::operator()(), plot(), and test_lda().
◆ fxc_apply()
| std::vector< madness::Tensor< double > > madness::XCfunctional::fxc_apply | ( | const std::vector< madness::Tensor< double > > & | t, |
| const int | ispin | ||
| ) | const |
compute the second derivative of the XC energy wrt the density and apply
Return the following quantities (RHF only) (see Yanai2005, Eq. (13))
![\begin{eqnarray*}
\mbox{result[0]} &:& \qquad \frac{\partial^2 \epsilon}{\partial \rho^2} \rho_\mathrm{pt}
+ 2.0 * \frac{\partial^2 \epsilon}{\partial \rho\partial\sigma}\sigma_\mathrm{pt}\\
\mbox{result[1-3]} &:& \qquad 2.0 * \frac{\partial\epsilon}{\partial\sigma}\nabla\rho_\mathrm{pt}
+ 2.0 * \frac{\partial^2\epsilon}{\partial\rho\partial\sigma} \rho_\mathrm{pt}\nabla\rho
+ 4.0 * \frac{\partial^2\epsilon}{\partial^2\sigma} \sigma_\mathrm{pt}\nabla\rho
\end{eqnarray*}](form_370.png)
- Parameters
-
[in] t The input densities and derivatives as required by the functional, as in the xc_arg enum [in] ispin not referenced since only RHF is implemented, always 0
- Returns
- a vector of Functions containing the contributions to the kernel apply
References MADNESS_EXCEPTION.
Referenced by madness::xc_kernel_apply::operator()().
◆ get_ggatol()
|
inline |
return the binary munging threshold for the final result in the GGA potential/kernel
the GGA potential will be munged based on the smallness of the original density, which we call binary munging
References ggatol.
◆ get_rhotol()
|
inline |
return the munging threshold for the density
References rhotol.
◆ has_fxc()
| bool madness::XCfunctional::has_fxc | ( | ) | const |
Returns true if the second derivative of the functional is available (not yet supported)
◆ has_kxc()
| bool madness::XCfunctional::has_kxc | ( | ) | const |
Returns true if the third derivative of the functional is available (not yet supported)
◆ hf_exchange_coefficient()
|
inline |
Returns the value of the hf exact exchange coefficient.
References hf_coeff.
Referenced by madness::SCF::apply_potential().
◆ initialize()
| void madness::XCfunctional::initialize | ( | const std::string & | input_line, |
| bool | polarized, | ||
| World & | world, | ||
| const bool | verbose = false |
||
| ) |
Initialize the object from the user input data.
- Parameters
-
[in] input_line User input line (without beginning XC keyword) [in] polarized Boolean flag indicating if the calculation is spin-polarized
References e(), hf_coeff, rhomin, rhotol, and spin_polarized.
Referenced by MiniDFT::MiniDFT(), madness::SCF::SCF(), main(), test_lda(), and test_xcfunctional().
◆ is_dft()
| bool madness::XCfunctional::is_dft | ( | ) | const |
Returns true if there is a DFT functional (false probably means Hatree-Fock exchange only)
References is_gga(), is_lda(), and is_meta().
Referenced by madness::SCF::apply_potential().
◆ is_gga()
| bool madness::XCfunctional::is_gga | ( | ) | const |
Returns true if the potential is gga (needs first derivatives)
Referenced by madness::XCOperator< T, NDIM >::apply_xc_kernel(), madness::xc_potential::get_result_size(), madness::xc_kernel_apply::get_result_size(), is_dft(), plot(), madness::XCOperator< T, NDIM >::prep_xc_args(), madness::XCOperator< T, NDIM >::prep_xc_args_response(), and test_xcfunctional().
◆ is_lda()
| bool madness::XCfunctional::is_lda | ( | ) | const |
Returns true if the potential is lda.
References hf_coeff.
Referenced by madness::xc_potential::get_result_size(), and is_dft().
◆ is_meta()
| bool madness::XCfunctional::is_meta | ( | ) | const |
Returns true if the potential is meta gga (needs second derivatives ... not yet supported)
Referenced by is_dft().
◆ is_spin_polarized()
|
inline |
Returns true if the functional is spin_polarized.
References spin_polarized.
Referenced by madness::SCF::apply_potential(), madness::XCOperator< T, NDIM >::apply_xc_kernel(), madness::Coulomb< double, 3 >::compute_potential(), madness::xc_potential::get_result_size(), plot(), madness::XCOperator< T, NDIM >::prep_xc_args(), madness::XCOperator< T, NDIM >::prep_xc_args_response(), and test_xcfunctional().
◆ make_libxc_args()
|
protected |
convert the raw density (gradient) data to be used by the xc operators
Involves mainly munging of the densities and multiplying with 2 if the calculation is spin-restricted. Response densities and density gradients are munged based on the value of the ground state density, since they may become negative and may also be much more diffuse. dimensions of the output tensors are for spin-restricted and unrestricted (with np the number of grid points in the box): rho(np) or rho(2*np) sigma(np) sigma(3*np) rho_pt(np) sigma_pt(2*np)
- Parameters
-
[in] t input density (gradients) [out] rho ground state (spin) density, properly munged [out] sigma ground state (spin) density gradients, properly munged [out] rho_pt response density, properly munged (no spin) [out] sigma_pt response (spin) density gradients, properly munged [out] drho density derivative, constructed from rho and zeta [out] drho_pt response density derivative directly from xc_args [in] need_response flag if rho_pt and sigma_pt need to be calculated
References MADNESS_EXCEPTION.
◆ munge()
|
inlineprivate |
◆ munge_old()
|
inlinestatic |
◆ plot()
|
inline |
Crude function to plot the energy and potential functionals.
References e(), enum_rhoa, enum_rhob, enum_saa, exc(), madness::f, is_gga(), is_spin_polarized(), lo, and vxc().
◆ polyn()
|
inlinestaticprotected |
◆ vxc()
| std::vector< madness::Tensor< double > > madness::XCfunctional::vxc | ( | const std::vector< madness::Tensor< double > > & | t, |
| const int | ispin | ||
| ) | const |
Computes components of the potential (derivative of the energy functional) at np points.
Any HF exchange contribution must be separately computed. Items in the vector argument t are interpreted similarly to the xc_arg enum.
We define 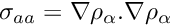
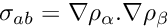
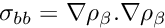
For unpolarized GGA, matrix elements of the potential are
![\[
< \phi | \hat V | \psi > = \int \left( \frac{\partial \epsilon}{\partial \rho} \phi \psi
+ \left( 2 \frac{\partial \epsilon}{\partial \sigma} \right)
\nabla \rho \cdot \nabla \left( \phi \psi \right) \right) dx
\]](form_365.png)
For polarized GGA, matrix elements of the potential are
![\[
< \phi_{\alpha} | \hat V | \psi_{\alpha} > = \int \left( \frac{\partial \epsilon}{\partial \rho_{\alpha}} \phi \psi
+ \left( 2 \frac{\partial \epsilon}{\partial \sigma_{\alpha \alpha}} \nabla \rho_{\alpha}
+ \frac{\partial \epsilon}{\partial \sigma_{\alpha \beta}} \nabla \rho_{\beta} \right) . \nabla \left( \phi \psi \right) \right) dx
\]](form_366.png)
Integrating the above by parts and assuming free-space or periodic boundary conditions we obtain that the local multiplicative form of the GGA potential is
![\[
V_{\alpha} = \frac{\partial \epsilon}{\partial \rho_{\alpha}}
- \left(\nabla . \left(2 \frac{\partial \epsilon}{\partial \sigma_{\alpha \alpha}} \nabla \rho_{\alpha}
+ \frac{\partial \epsilon}{\partial \sigma_{\alpha \beta}} \nabla \rho_{\beta} \right) \right)
\]](form_367.png)
Return the following quantities for RHF: (see Yanai2005, Eq. (12))
![\begin{eqnarray*}
\mbox{result[0]} &:& \qquad \frac{\partial \epsilon}{\partial \rho} \\
\mbox{result[1-3]} &:& \qquad 2 \rho \frac{\partial \epsilon}{\partial \sigma} \nabla\rho
\end{eqnarray*}](form_368.png)
and for UHF same-spin and other-spin quantities
![\begin{eqnarray*}
\mbox{result[0]} &:& \qquad \frac{\partial \epsilon}{\partial \rho_{\alpha}} \\
\mbox{result[1-3]} &:& \qquad \rho_\alpha \frac{\partial \epsilon}{\partial \sigma_{\alpha \alpha}} \nabla\rho_\alpha\\
\mbox{result[4-6]} &:& \qquad \rho_\alpha \frac{\partial \epsilon}{\partial \sigma_{\alpha \beta}} \nabla\rho_\beta
\end{eqnarray*}](form_369.png)
- Parameters
-
[in] t The input densities and derivatives as required by the functional [in] ispin Specifies which component of the potential is to be computed as described above
- Returns
- the requested quantity, based on ispin (0: same spin, 1: other spin)
References madness::c_rks_vwn5__(), madness::c_uks_vwn5__(), madness::f, std::isnan(), MADNESS_PRAGMA_CLANG, munge(), madness::pop(), madness::print(), madness::Tensor< T >::ptr(), q(), spin_polarized, v, madness::x_rks_s__(), madness::x_uks_s__(), and madness::xf().
Referenced by madness::xc_potential::operator()(), plot(), test_lda(), and test_xcfunctional().
Member Data Documentation
◆ ggatol
|
protected |
See initialize and munge*.
Referenced by get_ggatol().
◆ hf_coeff
|
protected |
Factor multiplying HF exchange (+1.0 gives HF)
Referenced by hf_exchange_coefficient(), initialize(), and is_lda().
◆ nderiv
|
protected |
the number of xc kernel derivatives (lda: 0, gga: 1, etc)
◆ number_xc_args
|
static |
max number of intermediates
Referenced by madness::XCOperator< T, NDIM >::prep_xc_args().
◆ rhomin
|
protected |
Referenced by XCfunctional(), binary_munge(), initialize(), and munge().
◆ rhotol
|
protected |
See initialize and munge*.
Referenced by XCfunctional(), get_rhotol(), initialize(), and munge().
◆ spin_polarized
|
protected |
True if the functional is spin polarized.
Referenced by exc(), initialize(), is_spin_polarized(), and vxc().
The documentation for this class was generated from the following files:
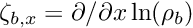
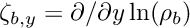
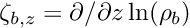
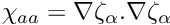
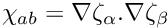
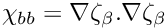
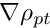


![\[
f(x,x_{\mathrm{min}},x_{\mathrm{max}}) = \left\{
\begin{array}{ll}
x_{\mathrm{min}} & x < x_{\mathrm{min}} \\
p(x,x_{\mathrm{min}},x_{\mathrm{max}}) & x_{\mathrm{min}} \leq x_{\mathrm{max}} \\
x & x_{\mathrm{max}} < x
\end{array}
\right.
\]](form_355.png)