Collaboration diagram for Chemistry:

Background

MADNESS does quantum chemistry

DFT functionals for the user

A molecular wave function may be determined using the ground state density only. For all but the simplest local density approximation functionals we use the density functional library libxc. The user may request a functional according to the general syntax

xc FUNC1 weight1 FUNC2 weight2 ..

xc

XCfunctional xc

Definition newsolver_lda.cc:53

where FUNC1 etc are the name of a libxc functional, and the weight describes the admixture coefficient

or use the following predefined functionals (not case sensitive)

xc hf
xc lda
xc bp
xc pbe
xc pbe0
xc b3lyp

As an example, the PBE0 functional would be expressed in the general syntax as

xc GGA_X_PBE 0.75 GGA_C_PBE 1.0 HF 0.25

Expert parameters are RHOTOL, RHOMIN, and GGATOL, which determine at which density value threshold (RHOTOL) the density will be set to RHOMIN inside libxc, and at which density the gga potential will be munged, since it might not be bound.

DFT functionals for the developer

A DFT functional is most easily constructed through the use of the madness::XCOperator class in SCFOperators.h

#include "SCFOperators.h"

XCOperator xc_operator(world,&calc,ispin);

SCFOperators.h

Operators for the molecular HF and DFT code.

where the arguments to the constructor are the world and a pointer to a madness::SCF or madness::Nemo calculation. The constructor will create the necessary density and density gradients (in XCOperator::prep_xc_args() ). Note that the ispin argument (0 for alpha, 1 for beta) is only important for the computation of the xc potential, and may be changed later on to avoid re-creation of the density (gradients). The functional information is passed to the constructor through the calculation parameters.

A DFT energy and potential can be constructed as

double ex_energy=xc_operator.compute_xc_energy();

real_function_3d xc_potential=xc_operator.make_xc_potential();

Direct application of the XC functional to a vector of orbitals mo may be accomplished as

std::vector<real_function_3d> vmo = xc_operator(mo);

If a response kernel is requested (e.g. in CPHF equations, or in linear response), the kernel itself is numerically unstable. To some extent this instability is circumvented by performing as many operations as possible on a fixed grid, so that only the result of the kernel application is available

real_function_3d result=xc_operator.apply_xc_kernel(perturbed_density);

Internal implementation details

For LDA functionals the density is processed as-is, only very small and negative densities are set to zero (through the RHOTOL and RHOMIN arguments).

For GGA functionals the reduced density gradients 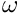$\sigma$ are necessary, which decay very fast and cause numerical instabilites. To avoid these instabilities we express the density gradients as

$\rho = exp(\zeta) \\ \nabla \rho = \rho \nabla \zeta \\ \sigma = |\nabla\rho|^2 = |\nabla \zeta|^2 \rho^2 = \chi \rho^2$

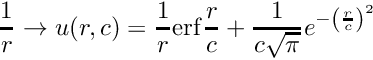
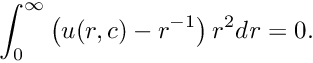
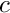
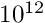
which defines the quantities $\zeta$ and $\chi$ . The functional form of $\zeta$ is a superposition of cones located at the nuclei with asymptotic slope of the HOMO orbital energy, its derivative is numerically more stable than that of the density itself. In this way the density gradients and the density may be munged in a consistent manner. In fact, often the ratio $\sigma/\rho^2 =\chi$ is used in DFT functionals. All functions are passed to libxc through the madness::XCfunctional interface class. A vector of functions named xc_arg is passed to the multiop method, with the various functions being on enumerated vector positions, described in madness::XCfunctional::xc_arg.

Response kernels for GGA are even more numerically unstable than the XC potential. We use the same log-derivative trick as before, which fixes the long-range noise. However the intermediate potentials have to be multiplied with the gradients of the (perturbed) density, followed by taking the divergence, which is equivalent to applying the Laplacian to the (perturbed) density. Numerical noise is amplified and convergence during the SCF or CPHF iterations might not be achieved. Furthermore, the perturbed density is not strictly positive, so its logarithm is not defined. We can pull an unperturbed density out of the perturbed density gradient to regain some stability

$\sigma_\mathrm{pt}=\nabla\rho\cdot\nabla\rho_\mathrm{pt} = \rho\left(\nabla\zeta\cdot\nabla\rho_\mathrm{pt}\right)$

The code in XCOperator works as follows

compute $\zeta$ , density gradients, etc through madness::XCOperator::prep_xc_args and put them on a vector of functions. So far these are spin densities.
call xc_potential or xc_kernel_apply
- call madness::XCfunctional::make_libxc_args to munge the density and density gradients – convert spin density to full density if spin-restricted
- call libxc functions to compute the functional derivatives of the density functional
- multiply intermediate quantities to the functional derivatives
- return scalar intermediates, for the exact description see in madness::XCfunctional::vxc and madness::XCfunctional::fxc_apply
multiply the semilocal intermediates with the density gradients, take div operator