A paraboloid (3 dimensions) More...

#include <sdf_shape_3D.h>

Inheritance diagram for madness::SDFParaboloid:

Collaboration diagram for madness::SDFParaboloid:

[legend]

Public Member Functions
	SDFParaboloid (const double c, const coord_3d &apex, const coord_3d &direc)
	Constructor for paraboloid.

coord_3d	grad_sdf (const coord_3d &pt) const
	Computes the gradient of the SDF.

double	sdf (const coord_3d &pt) const
	Computes the normal distance.

Public Member Functions inherited from madness::SignedDFInterface< 3 >
virtual	~SignedDFInterface ()

virtual Vector< double, NDIM >	grad_sdf (const Vector< double, NDIM > &x) const=0
	Returns the gradient of the signed distance from the surface (i.e., `dsdf(x)/dx`[i] )

virtual double	sdf (const Vector< double, NDIM > &x) const=0
	Returns the signed distance from the surface,.

Protected Member Functions
long double	eval_cubic (const long double x, const long double c, const long double d, const long double z) const
	Evaluates the cubic equation for the Lagrangian multipliers.

long double	eval_cubic_deriv (const long double x, const long double c, const long double d, const long double z) const
	Evaluates the derivative of the cubic equation for the Lagrangian multipliers.

long double	find_root (long double lower, long double upper, const long double c, const long double d, const long double z, bool dir) const

std::vector< long double >	get_roots (const long double c, const long double d, const long double z) const
	Finds real root(s) of the cubic polynomial in the sdf function.

Protected Attributes
const coord_3d	apex
	The apex.

const double	c
	Curvature/radius of the surface.

const coord_3d	dir
	The direction of the axis, from the apex INSIDE.

const long double	rootzero
	Numerical zero for the roots.

const long double	zero
	Numerical zero for root-finding in sdf.

Detailed Description

A paraboloid (3 dimensions)

The surface is defined by

$x^2 + y^2 - c * z == 0$

where is along the paraboloid's axis.

Constructor & Destructor Documentation

◆ SDFParaboloid()

madness::SDFParaboloid::SDFParaboloid	(	const double	c,
		const coord_3d &	apex,
		const coord_3d &	direc
	)

inline

Constructor for paraboloid.

Parameters

c	Parameter 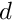in the definition of the paraboloid
apex	Apex of paraboloid
direc	Oriented axis of the paraboloid

Member Function Documentation

◆ eval_cubic()

long double madness::SDFParaboloid::eval_cubic	(	const long double	x,
		const long double	c,
		const long double	d,
		const long double	z
	)		const

inlineprotected

Evaluates the cubic equation for the Lagrangian multipliers.

Cubic equation of interest: d + c(2z+c/2)*L - c(c+z)L^2 + c^2/2L^3 == 0

Parameters

[in]	x	Value at which to evaluate.
[in]	c	Parameter c for the paraboloid.
[in]	d	The d parameter: x^2+y^2-cz = d
[in]	z	The distance from the apex along the paraboloid's axis (called dotp in sdf)

Returns: the value

References c, and d.

Referenced by find_root(), and get_roots().

◆ eval_cubic_deriv()

long double madness::SDFParaboloid::eval_cubic_deriv	(	const long double	x,
		const long double	c,
		const long double	d,
		const long double	z
	)		const

inlineprotected

Evaluates the derivative of the cubic equation for the Lagrangian multipliers.

Cubic equation of interest: d + c(2z+c/2)*L - c(c+z)L^2 + c^2/2L^3 == 0

Derivative: c(2z+c/2) - 2c(c+z)L + 3c^2/2 L^2

Parameters

[in]	x	Value at which to evaluate.
[in]	c	Parameter c for the paraboloid.
[in]	d	The d parameter: x^2+y^2-cz = d
[in]	z	The distance from the apex along the paraboloid's axis (called dotp in sdf)

Returns: the value

References c.

◆ find_root()

long double madness::SDFParaboloid::find_root	(	long double	lower,
		long double	upper,
		const long double	c,
		const long double	d,
		const long double	z,
		bool	dir
	)		const

inlineprotected

Finds a root in the specified range for the cubic equation.

This uses a simple bisection method... perhaps someone will improve it one day...

Parameters

[in]	lower	The bottom of the range
[in]	upper	The top of the range
[in]	c	Parameter c for the paraboloid.
[in]	d	The d parameter: x^2+y^2-cz = d
[in]	z	The distance from the apex along the paraboloid's axis (called dotp in sdf)
[in]	dir	True if the function is increasing in the domain, false for decreasing

Returns: the root.

References std::abs(), c, d, dir, eval_cubic(), lower, rootzero, upper, and zero.

Referenced by get_roots().

◆ get_roots()

std::vector< long double > madness::SDFParaboloid::get_roots	(	const long double	c,
		const long double	d,
		const long double	z
	)		const

inlineprotected

Finds real root(s) of the cubic polynomial in the sdf function.

The cubic equation can successfully solve the cubic analytically, but evaluating the expression can be numerically irksome. Analytical results show that at most one root appears in each of the domains

(-Infinity, (2z+2c-|c-2z|)/(3c))
((2z+2c-|c-2z|)/(3c), (2z+2c+|c-2z|)/(3c))
((2z+2c-|c-2z|)/(3c), Infinity).

Furthermore, the cubic is always increasing in the first and third domains, and always decreasing in the second.

Since the cubic is easy to evaluate, we use simple bisections to find the roots... this can probably be improved.

Cubic equation of interest: d + c(2z+c/2)*L - c(c+z)L^2 + c^2/2L^3 == 0

Parameters

[in]	c	Parameter c for the paraboloid.
[in]	d	The d parameter: x^2+y^2-cz = d
[in]	z	The distance from the apex along the paraboloid's axis (called dotp in sdf)

Returns: The root(s)

References std::abs(), c, d, eval_cubic(), find_root(), lower, upper, and zero.

Referenced by sdf().

◆ grad_sdf()

coord_3d madness::SDFParaboloid::grad_sdf ( const coord_3d & pt ) const

inline

Computes the gradient of the SDF.

Parameters

pt	Point at which to compute the gradient

Returns: the gradient

References MADNESS_EXCEPTION.

◆ sdf()

double madness::SDFParaboloid::sdf ( const coord_3d & pt ) const

inline

Computes the normal distance.

This SDF is exact.

Given a point, pt=(x, y, z), the goal is to find another point, pt0=(x0, y0, z0), on the surface that minimizes |pt - pt0|^2. The root of this minimized square distance (and a sign) is the sdf.

For simplicity (here), I will assume that the paraboloid's axis is along the positive z-axis and that the origin is the apex. Note that the code does NOT make these assumptions.

Thus, we want to minimize (x-x0)^2 + (y-y0)^2 + (z-z0)^2 subject to x0^2 + y0^2 - c z0 == 0.

Using Lagrange multipliers, the system of equations is -2(x-x0) == L 2 x0 -2(y-y0) == L 2 y0 -2(z-z0) == L (-c) x0^2 + y0^2 - c z0 == 0.

After some algebra, we get a cubic equation for L, (x^2 + y^2 - c z) + (2c z + c^2/2) L - c (z + c) L^2

c^2/2 L^3 == 0

This can be solved analytically in Mathematica, producing a long, messy equation. This equation has some stability issues (large cancellations in some areas) and is not implemented below. Instead we use an iterative root finder to locate the roots of the cubic. The simple bisection method is used, perhaps someone will improve the code someday).

Once we have the correct Lagrange multiplier, |pt - pt0|^2 = c L^2 (z - L c/2 + c/4). The square root of this quantity (with the appropriate sign for inside/outside) gives the sdf.

Parameters

pt	Point at which to compute the distance from the surface

Returns: The signed distance from the surface

References std::abs(), apex, c, d, diff(), dir, dist(), get_roots(), MADNESS_ASSERT, and upper.

Member Data Documentation

◆ apex

const coord_3d madness::SDFParaboloid::apex

protected

The apex.

Referenced by sdf().

◆ c

const double madness::SDFParaboloid::c

protected

Curvature/radius of the surface.

Referenced by eval_cubic(), eval_cubic_deriv(), find_root(), get_roots(), and sdf().

◆ dir

const coord_3d madness::SDFParaboloid::dir

protected

The direction of the axis, from the apex INSIDE.

Referenced by find_root(), and sdf().

◆ rootzero

const long double madness::SDFParaboloid::rootzero

protected

Numerical zero for the roots.

Referenced by find_root().

◆ zero

const long double madness::SDFParaboloid::zero

protected

Numerical zero for root-finding in sdf.

Referenced by find_root(), and get_roots().

The documentation for this class was generated from the following file:

sdf_shape_3D.h

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

◆ SDFParaboloid()

Member Function Documentation

◆ eval_cubic()

◆ eval_cubic_deriv()

◆ find_root()

◆ get_roots()

◆ grad_sdf()

◆ sdf()

Member Data Documentation

◆ apex

◆ c

◆ dir

◆ rootzero

◆ zero