Defines and implements the tensor train decomposition as described in I.V. Oseledets, Siam J. Sci. Comput. 33, 2295 (2011). More...
#include <madness/tensor/tensor.h>#include <madness/tensor/srconf.h>#include <madness/tensor/clapack.h>#include <madness/tensor/tensor_lapack.h>#include <madness/fortran_ctypes.h>#include <madness/world/archive.h>
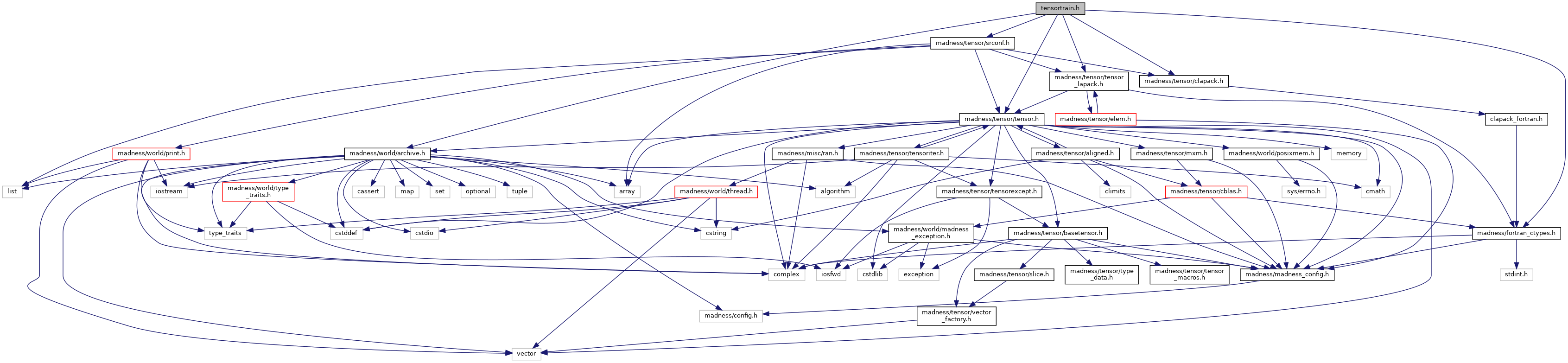
Include dependency graph for tensortrain.h:
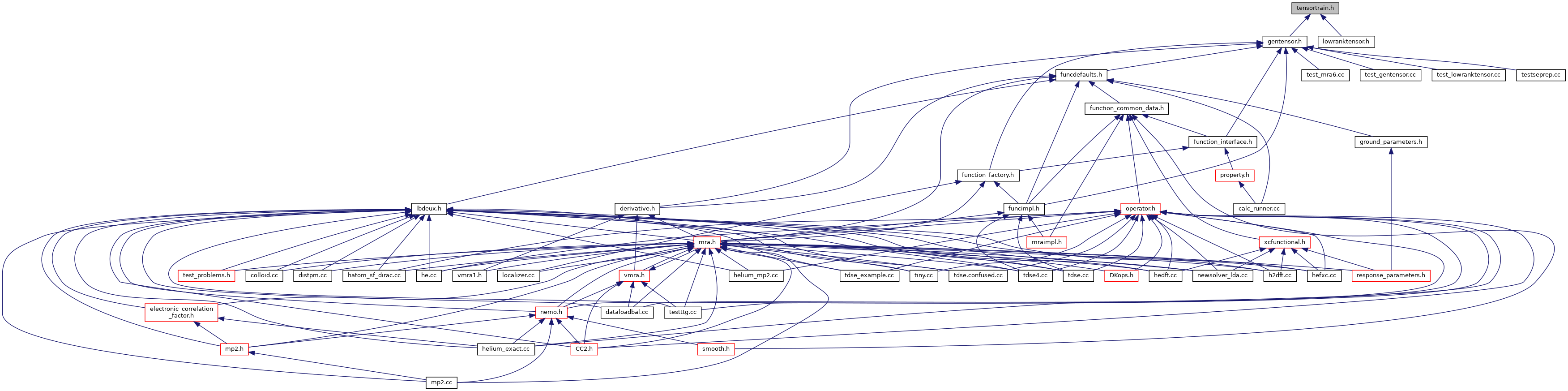
This graph shows which files directly or indirectly include this file:
Go to the source code of this file.
Classes | |
| class | madness::TensorTrain< T > |
Namespaces | |
| namespace | madness |
| Namespace for all elements and tools of MADNESS. | |
Functions | |
| template<class T , class Q > | |
| TensorTrain< TENSOR_RESULT_TYPE(T, Q)> | madness::apply (const TensorTrain< T > &op, const TensorTrain< Q > &t, const double thresh) |
| apply an operator in TT format on a tensor in TT format | |
| template<class T , class Q > | |
| TensorTrain< TENSOR_RESULT_TYPE(T, Q)> | madness::general_transform (const TensorTrain< T > &t, const Tensor< Q > c[]) |
| Transform all dimensions of the tensor t by distinct matrices c. | |
| template<class T , class Q > | |
| TensorTrain< TENSOR_RESULT_TYPE(T, Q)> | madness::outer (const TensorTrain< T > &t1, const TensorTrain< Q > &t2) |
| computes the outer product of two tensors | |
| template<typename T > | |
| long | madness::rank_revealing_decompose (Tensor< T > &A, Tensor< T > &U, const double thresh, Tensor< typename Tensor< T >::scalar_type > &s, Tensor< T > &scr) |
| template<class T , class Q > | |
| TensorTrain< TENSOR_RESULT_TYPE(T, Q)> | madness::transform (const TensorTrain< T > &t, const Tensor< Q > &c) |
| transform each dimension with the same operator matrix | |
| template<class T , class Q > | |
| TensorTrain< TENSOR_RESULT_TYPE(T, Q)> | madness::transform_dir (const TensorTrain< T > &t, const Tensor< Q > &c, const int axis) |
| Transforms one dimension of the tensor t by the matrix c, returns new contiguous tensor. | |
| template<typename T > | |
| TensorTrain< T > | madness::tt_identity (const long ndim, const long k) |
| compute the n-D identity operator with k elements per dimension | |
Detailed Description
Defines and implements the tensor train decomposition as described in I.V. Oseledets, Siam J. Sci. Comput. 33, 2295 (2011).