Collaboration diagram for MADNESS functions:

Defaults for functions

Default values for all function and operator attributes are stored in the FunctionDefaults class. This is actually a template so that different values can be set for functions with different numbers of dimensions. We saw earlier that

FunctionDefaults<1>::set_cubic_cell(0,10);

sets the user's simulation cell as . Presently, all functions of a given dimension must share the same cell. Other common attributes are

k – the wavelet order. A practical rule of thumb is if the default truncation threshold is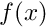 $10^{-n}$ , then the order should be chosen as . The default is 6.
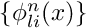
thresh – the truncation threshold. The default is 1e-4.
bc – the boundary conditions. See below for more details. The default is free.

Boundary conditions

In MADNESS, boundary conditions are associated with operators, not functions, and the boundary conditions are imposed on the surface enclosing the entire simulation volume. That is, they are exterior boundary conditions. For derivative operators the following conditions are understood, and can be imposed separately on each surface

BC_ZERO – Zero Dirichlet
BC_PERIODIC – Periodic (both left and right surfaces must agree on this value)
BC_FREE – Free (default)
BC_DIRICHLET – General Dirichlet (requires provision of one or more functions)
BC_ZERONEUMANN – Zero Neumann
BC_NEUMANN – General Neumann (requires provision of one or more functions)

For integral operators only periodic and free-space conditions are understood – BC_PERIODIC yields periodic and all other conditions yield free-space.

Example: to make the default boundary conditions in 3D

BoundaryConditions<3> bc(BC_FREE);

Example: to make boundary conditions in 3D with zero Dirichlet in 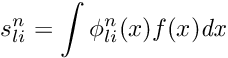and and periodic in ,

BoundaryConditions<3> bc(BC_ZERO);
 
bc(2,0) = bc(2,1) = BC_PERIODIC;

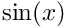
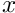
Example: to override the default boundary conditions with yours in a variable named bc in 3D

FunctionDefaults<3>::set_bc(bc);

Differentiation, multiplication, inner products

We now examine operations such as differentiation, multiplication, and inner products. A relevant simple example is trunk/src/examples/hatom_energy.cc.

Differentiation

Differentiation is performed by applying a differential operator to a function. The operator is constructed with desired the boundary conditions and direction for differentiation (directions are indexed starting from zero, so in 3D x=0, y=1, and z=2). The operators can be kept for repeated application, or made and discarded after use.

For example, to make the derivative operator in 3D with respect to the first variable using boundary conditions from FunctionDefaults, and to apply it to functions f, g and h:

real_derivative_3d Dx(world, 0); 
real_function_3d dfdx = Dx(f); 
real_function_3d dgdx = Dx(g); 
real_function_3d dhdx = Dx(h); 

Multiplication, addition, subtraction of functions

Most simple mathematical operations can be composed in MADNESS as they are normally written in standard notation. For instance, if f, g and h are functions the expression

$f(x) = 2g(x) + 3h(x) - 7g(x)h(x) + 99$

is transcribed as

f = 2*g + 3*h - 7*g*h + 99;

where * indicates point-wise multiplication of functions.

Attention: Addition and subtraction of functions are exact operations in the sense that the result can be exactly represented in the MADNESS basis. Multiplication is inexact since the product of two polynomials of order is of order . The auto-refinement algorithm within MADNESS is still under development – please refer to the implementation notes for more detail.

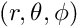
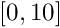
Inner products

The inner product of two functions is defined as

$\left( f \left| g \right. \right) = \int f(x)^\textrm{*} g(x) dx,$

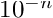
where $\textrm{*}$ indicates complex conjugation and the integral is taken over the entire simulation volume. The above is computed for two MADNESS functions f and g of the same type using

inner(f, g);

inner

std::complex< double > inner(const Fcwf &psi, const Fcwf &phi)

Definition fcwf.cc:275

If the input functions are real, the result is real; for complex functions the result is complex.

Integral operators

The Poisson equation

$\nabla^{2} u = -4\pi \rho$

is ubiquitous in scientific and engineering simulations. For the sake of simplicity, we assume free-space boundary conditions (zero at infinity), such that the Green's function is just 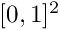$1/\left| r \right|$ . If the right-hand side of the Poisson equation is rho, then the Poisson equation can be solved in MADNESS as

real_convolution_3d op = CoulombOperator(world, 0.001, 1e-6);
 
real_function_3d result = op(rho);

This is employed by many codes in the examples directory. The call to CoulombOperator builds a low-separation rank approximation (see the implementation notes) of the Green's function for the Poisson equation. The approximation is accurate to 1e-6 from a smallest length scale of 0.001 to the entire box size.

If you have more complicated boundary conditions which require single or double layer terms please refer the example in trunk/src/examples/interior_dirichlet.cc for more details.

Operations on vectors of functions

The header file madness/mra/vmra.h defines operations on vectors of functions. These are convenient in eliminating error-prone loops over arrays/vectors of functions, and the vector operations are much more efficient since many operations can occur in parallel. The example code trunk/src/examples/vnucso.cc and the molecular density functional code make extensive use of the vector API (application programming interface) to solve eigenproblems. Let us discuss this in more detail.

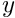
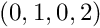
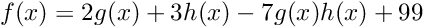
Given a subspace defined by a vector of functions, $f_{i}(x),\; i=0, \ldots, n-1$ we can diagonalize the operator $\hat{H}$ in the subspace by constructing the matrix representations of the operator ( $\mathbf{H}$ ) and metric ( $\mathbf{S}$ ):

$\begin{eqnarray*} \mathbf{H}_{ij} & = & \left< f_i \left| \hat{H} \right| f_j \right> \\ \mathbf{S}_{ij} & = & \left< f_i \left| \right. f_j \right>, \end{eqnarray*}$

and then solving the generalized eigenvalue problem

$\mathbf{HC}=\mathbf{SC}E$

to obtain the eigenvalues and coefficients in the subspace. The eigenfunctions $u_{i}(x)$ are obtained by transforming the original basis

$\mathbf{u}=\mathbf{fC} \qquad \mathrm{or} \qquad u_{i}(x) = \sum _{j} f_{j}(x) \mathbf{c}_{ji}$

Given an STL vector of 3D functions, f, and another Hf containing the result of applying the operator 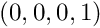$\hat{H}$ to the vector, the above is compactly translated into MADNESS as

real_tensor H = matrix_inner(world, f, Hf); 
real_tensor S = matrix_inner(world, f, f); 
real_tensor C, E; 
 
sygv(H, S, 1, C, E); 
vector_real_function_3d evec = transform(world, f, C); 

The matrix_inner() routine computes the matrix of inner products (or matrix elements) of two vectors of functions, and the sygv() routine (in linalg/tensor_lapack.h) is a wrapper around the LAPACK real symmetric and complex Hermitian generalized eigenvalue routines. Finally, the transform() routine transforms the basis to compute the eigenfunctions.

Previous: Compiling and running MADNESS programs; Next: Input/Output