
Additional documentation and instructions exist in several places:
For basic computing with MADNESS functions, the only header file that you should need to include is <mra/mra.h>. Advanced programs may need a few others. You should include the directory in the include path to avoid possible conflicts with similarly named files from other packages. In the following documentation trunk will denote the top-level directory of the MADNESS distribution.
- From math to C++ to numerical computation
A perhaps more up to date version of this example is here.
This section shows you how to use MADNESS and evaluate a simple mathematical expression, notably this one dimensional integral.
![\[
\int_{0}^{10} \sin (x) \mathit{dx} = 1 - \cos(10) \doteq 1.8390715
\]](form_67.png)
The corresponding code is in trunk/src/examples/sininteg.cc, and we will go through this first example in gory detail. The main steps will be
- translating the function from math to C++ to be called by MADNESS
- initializing the MADNESS parallel runtime
- initializing the MADNESS numerical environment
- generating a numerical representation from the C++ function
- computing the integral
- printing the result
- terminating the MADNESS parallel runtime
- compiling your program
- running your program
- Step 1 – translating from Math to C++
MADNESS generates a numerical representation of a function ( 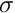
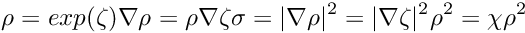
![\[
s_{li}^{n} = \int \phi _{li}^{n}(x) f(x) \mathit{dx}
\]](form_70.png)
using adaptive numerical quadrature. Thus, MADNESS has to be able to evaluate your function at an arbitrary point, and so you must provide it with a C++ implementation of your function using a standard interface. MADNESS passes to your function the coordinates (an array of the appropriate dimension) and you return the value. For simple functions, a C++ function suffices whereas more complicated stuff might require a C++ class (see a subsequent example).
For this example, we wish to evaluate the function 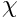
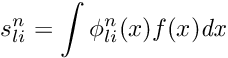
If your function were in 3-D it would be passed a coord_3d that would have 3 elements (0, 1, and 2) that you might interpret as 
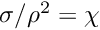
- Attention
- If your function contains discontinuities (in value or derivatives), noise, or singularities, special care is needed. This is discussed in more detail below, but the simple rule of thumb is your function should be accurate nearly to machine precision even if you only want to compute to much lower precision with MADNESS.
- MADNESS will call your function from multiple threads in order to use multi-core processors efficiently, so the code for your function should be thread safe. It should not modify static (Fortran keyword
save) or global (Fortran common blocks or modules) data; reading from such locations is fine. Note that this constraint applies to all code invoked by your function, including math, BLAS, and linear algebra libraries and for some machines/compilers it requires special options be used (the MADNESS makefiles look after this). If you suspect a thread problem, try running with the environment variableMAD_NUM_THREADSset to one. - If you are using the AMD math library ACML, do not set the environmental variable
OMP_NUM_THREADS(or set it to one).
- Steps 2, 3 and 7 – initializing and finalizing the MADNESS environment
MADNESS has its own parallel runtime environment that is fully compatible with the Message Passing Interface (MPI). Just as for MPI, the MADNESS runtime must be initialized at the start and cleaned up at the end. Here is the simplest parallel program using MADNESS.
The World object in MADNESS is similar to an MPI communicator (each World is associated with a communicator) but contains all of the information necessary to provide the rich functionality of the MADNESS runtime. Instead of calling MPI::Init() and MPI::Finalize(), a MADNESS program invokes madness::initialize() and madness::finalize() (call madness::initialized() to check that MADNESS had been initialized). The routine madness::startup() initializes the MADNESS numerical environment.
- Step 4 – generating a numerical representation
We implemented the C++ function above (myf) and the domain is specified by the problem as ![$x\in [0,10]$](form_74.png)
The first line sets the domain and the second makes a numerical representation of your function. The slightly unusual form of the constructor for a MADNESS function is called the "named parameter idiom." The first version of MADNESS was written in Python, which provides named parameters that can have default values. To override the default for some parameter only required specifying its name. However, C++ does not provide named parameters and the closest we can get to them is the above idiom. To make a Function what you are actually doing is making a FunctionFactory associated with a World, overriding defaults inside the factory, and then constructing a function from the factory. The default function is zero, so to make a zero 1D function we would just type
In the second line, to generate a MADNESS Function from your C++ function we override the default with the desired function pointer.
- Step 5 – computing the integral
The integral of a function over the whole domain is computed with the trace() function, c.f.,
- Attention
- This is a collective parallel operation. If you are running in parallel, the numerical representation of your function is distributed across multiple processors, so adding up the result requires collective communication (the equivalent of MPI's
All_reduce()). Therefore, every process associated with theWorldmust execute this statement; otherwise your program will hang if it is running in parallel using MPI.
- Step 6 – printing the result
If you only want to run sequentially, just print your data in any of the myriad ways possible using C++. However, if you ever want to run in parallel across multiple nodes using MPI you should from the outset get in the habit of writing the following instead
The critical ingredient is the if-test that ensures only one process actually does the printing (in this case process zero, but that choice is arbitrary). If you don't do this, your output will be unexpectedly verbose. The templated routine print() is just a convenience wrapper around cout << that automatically inserts spaces between elements and a newline at the end.
- Attention
- We assigned the result of
f.trace()to a variable becausetraceis a collective, but printing is serial. Anecdotally, at least 90% of hanging parallel programs are due to getting this wrong.
- The complete program
Your complete program, trunk/src/apps/sininteg.cc, looks like this
Yes, this is rather verbose for integrating 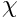
Previous: Getting started with MADNESS; Next: Compiling and running MADNESS programs