slymer::PrimitiveGaussian Class Reference

A primitive Gaussian function. More...

#include <gaussian.h>

Collaboration diagram for slymer::PrimitiveGaussian:

Public Member Functions
	PrimitiveGaussian ()
	Default constructor: Make the function 1 ( , ).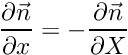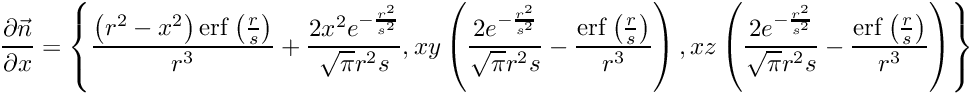
	PrimitiveGaussian (const GaussianType &type, const std::array< double, 3 > &center, const double ec)
	Create a primitive Gaussian function centered on the specific point, with the specified decay constant and type.
	PrimitiveGaussian (const PolynomialCoeffs &exppoly_, const PolynomialCoeffs &prefactor_)
	Create a primitive Gaussian function with the specified exponential polynomial (quadratic) and polynomial prefactor.
double	operator() (const std::array< double, 3 > &x) const
	Evaluate the Gaussian primitive at the specified point.
PrimitiveGaussian	operator* (const PrimitiveGaussian &rhs) const
	Multiply two primitive Gaussians. The result is another.

Protected Types
using	CF = std::tuple< PolynomialCoeffs, std::array< double, 3 >, std::array< double, 3 >, std::array< std::array< double, 3 >, 3 > >
	Return type for the function's canonical form.

Protected Attributes
PolynomialCoeffs	exppoly
	Coefficients in the exponent's quadratic function.
PolynomialCoeffs	prefactor
	Polynomial prefactor ( 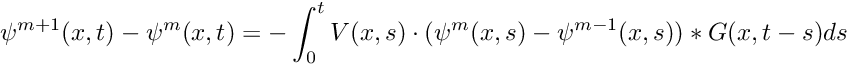in the class description).

Detailed Description

A primitive Gaussian function.

This basis function has the form

where is a polynomial and is the `‘center’' of the Gaussian and is the variance/covariance matrix.

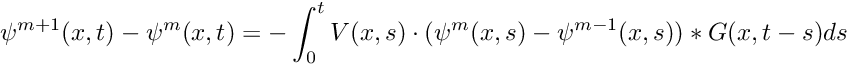
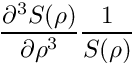
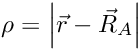
This class is designed to work with Gaussian basis functions in quantum chemistry codes, but is made to be a bit more general for other applications.

The wikipedia page on multivariable normal distributions may be helpful (https://en.wikipedia.org/wiki/Multivariate_normal_distribution).

Member Typedef Documentation

CF

using slymer::PrimitiveGaussian::CF = std::tuple<PolynomialCoeffs, std::array<double, 3>, std::array<double, 3>, std::array<std::array<double, 3>, 3> >

protected

Return type for the function's canonical form.

The first element is the polynomial prefactor, converted to use the principal coordinates. The second element is the array of decay values (eigenvalues of the covariance matrix). The third element is the 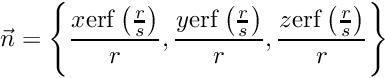vector (essentially the center of the Gaussian). The fourth element are the canonical axes in the original coordinates (for debugging purposes).

Constructor & Destructor Documentation

PrimitiveGaussian() [1/3]

slymer::PrimitiveGaussian::PrimitiveGaussian ( )

inline

Default constructor: Make the function 1 ( , ).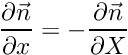

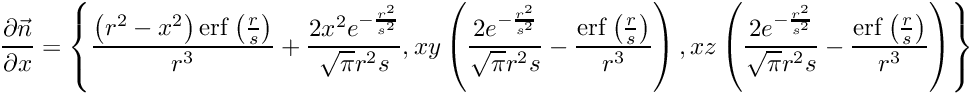
References prefactor.

PrimitiveGaussian() [2/3]

slymer::PrimitiveGaussian::PrimitiveGaussian	(	const GaussianType &	type,
		const std::array< double, 3 > &	center,
		const double	ec
	)

Create a primitive Gaussian function centered on the specific point, with the specified decay constant and type.

Exceptions

std::invalid_argument

if the decay constant is non-positive.

Parameters

[in]	type	The orbital type of the Gaussian.
[in]	center	The center of the Gaussian.
[in]	ec	The decay constant in the exponential.

References slymer::dxx, slymer::dxxmyy, slymer::dxy, slymer::dxz, slymer::dyy, slymer::dyz, slymer::dzz, slymer::dzzmrr, exppoly, slymer::fxxx, slymer::fxxy, slymer::fxxymyyy, slymer::fxxz, slymer::fxxzmyyz, slymer::fxyy, slymer::fxyymxxx, slymer::fxyz, slymer::fxzz, slymer::fxzzmrrx, slymer::fyyy, slymer::fyyz, slymer::fyzz, slymer::fyzzmrry, slymer::fzzz, slymer::fzzzmrrz, slymer::gx2my2dz2mr2, slymer::gx4mx2y2py4, slymer::gxxxx, slymer::gxxxy, slymer::gxxxz, slymer::gxxyy, slymer::gxxyz, slymer::gxxzz, slymer::gxydx2my2, slymer::gxydz2mr2, slymer::gxyyy, slymer::gxyyz, slymer::gxyzz, slymer::gxzdx2my2, slymer::gxzdz2mr2, slymer::gxzzz, slymer::gyyyy, slymer::gyyyz, slymer::gyyzz, slymer::gyzdx2my2, slymer::gyzdz2mr2, slymer::gyzzz, slymer::gzero, slymer::gzzzz, slymer::hm1, slymer::hm2, slymer::hm3, slymer::hm4, slymer::hm5, slymer::hp1, slymer::hp2, slymer::hp3, slymer::hp4, slymer::hp5, slymer::hxxxxx, slymer::hxxxxy, slymer::hxxxxz, slymer::hxxxyy, slymer::hxxxyz, slymer::hxxxzz, slymer::hxxyyy, slymer::hxxyyz, slymer::hxxyzz, slymer::hxxzzz, slymer::hxyyyy, slymer::hxyyyz, slymer::hxyyzz, slymer::hxyzzz, slymer::hxzzzz, slymer::hyyyyy, slymer::hyyyyz, slymer::hyyyzz, slymer::hyyzzz, slymer::hyzzzz, slymer::hzero, slymer::hzzzzz, norm(), pi, pow(), prefactor, slymer::px, slymer::py, slymer::pz, and slymer::s.

PrimitiveGaussian() [3/3]

slymer::PrimitiveGaussian::PrimitiveGaussian	(	const PolynomialCoeffs &	exppoly_,
		const PolynomialCoeffs &	prefactor_
	)

Create a primitive Gaussian function with the specified exponential polynomial (quadratic) and polynomial prefactor.

Exceptions

std::invalid_argument

if the exponential polynomial is not quadratic (or constant or linear as subsets).

Parameters

[in]	exppoly_	The exponential polynomial.
[in]	prefactor_	The degree of the prefactor.

References exppoly, and slymer::PolynomialCoeffs::get_degree().

Member Function Documentation

operator()()

double slymer::PrimitiveGaussian::operator()

(

const std::array< double, 3 > &

x

)

const

Evaluate the Gaussian primitive at the specified point.

Parameters

[in]

x

The point.

Returns

The Gaussian primitive evaluated at the point x.

References exppoly, and prefactor.

operator*()

PrimitiveGaussian slymer::PrimitiveGaussian::operator*

(

const PrimitiveGaussian &

rhs

)

const

Multiply two primitive Gaussians. The result is another.

Parameters

[in]

rhs

The right-hand object.

Returns

The product.

References exppoly, and prefactor.

Member Data Documentation

exppoly

PolynomialCoeffs slymer::PrimitiveGaussian::exppoly

protected

Coefficients in the exponent's quadratic function.

Referenced by PrimitiveGaussian(), PrimitiveGaussian(), operator()(), and operator*().

prefactor

PolynomialCoeffs slymer::PrimitiveGaussian::prefactor

protected

Polynomial prefactor ( 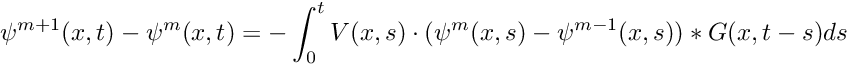in the class description).

Referenced by PrimitiveGaussian(), PrimitiveGaussian(), operator()(), and operator*().

---

The documentation for this class was generated from the following files:

• gaussian.h
• madness/chem/gaussian.cc