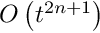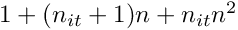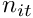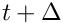The source is here.

Points of interest

high-order integration of general time-dependent problems
semigroup approach

Background

Given 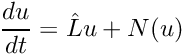, we seek to solve the PDE

$\frac{du}{dt} = \hat{L} u + N(u)$

for the function at some future time 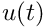(i.e., for ). $\hat{L}$ is a linear operator that we are able to exponentiate, and is everything else including linear and non-linear parts.

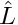
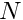
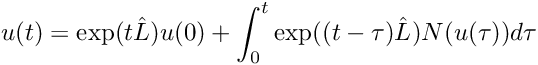
In the semigroup approach the formal solution to the PDE is written

$u(t) = \exp(t \hat{L} ) u(0) + \int_0^t \exp((t-\tau)\hat{L}) N(u(\tau)) d\tau$

Numerical quadrature of the integral using Gauss-Legendre quadrature points is used resulting in a set of equations that are iteratively solved (presently using simple fixed point iteration from a first-order explicit rule).

The user provides

functors to apply the exponential and non-linear parts, and
if necessary a user-defined data type that supports a copy constructor, assignment, inplace addition, multiplication from the right by a double, and computation of the distance between two solutions and with the api \verb+double distance(a,b)+

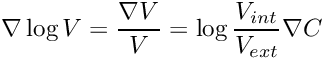
Have a look in testspectralprop.cc for example use.

With quadrature points, the error is $O\left(t^{2n+1}\right)$ and the number of applications of the exponential operator per time step is $1+(n_{it}+1)n +n_{it}n^2$ where $n_{it}$ is the number of iterations necessary to solve the equations (typically about 5 but this is problem dependent).