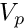The source is here.
- Points of interest
- application of a function of a function to exponentiate the potential
- use of a functor to compute the solution at an arbitrary future time
- convolution with the Green's function
- Background
This adds to the complexity of the other heat equation example by including a linear term. Specifically, we solve
![\[
\frac{\partial u(x,t)}{\partial t} = c \nabla^2 u(x,t) + V_p(x,t) u(x,t)
\]](form_159_dark.png)
If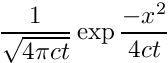 
![\[
G_0(x,t) = \frac{1}{\sqrt{4 \pi c t}} \exp \frac{-x^2}{4 c t}
\]](form_161_dark.png)
For non-zero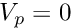 
![\[
G(x,t) = G_0(x,t/2) * \exp(V_p t) * G_0(x,t/2) + O(t^3)
\]](form_163_dark.png)
In order to form an exact solution for testing, we choose 
