
MADNESS is based on multiresolution analysis (MRA) and low-separation rank (LSR) approximations of functions and operators. It can be considered an adaptive spectral element method using a discontinuous and singular multiresolution basis. The representations of differential operators in the wavelet bases are provably similar to adaptive finite difference discretizations. Thus, the process of solving the resulting linear systems has similar behaviors to other adaptive methods. For example, the derivative operator and the Laplacian operator are unbounded operators. Thus the condition number, which often constrains how accurately the linear system can be solved, goes to infinity as the bases or the nets are refined. In order to solve these equations in practice, one has to precondition the system. Effective preconditioners are problem dependent and the theory of their construction is an area of on-going research.
The integral operator, which is the formal inverse associated with the differential operator, is usually bounded. MRA and LSR have been proven to be suitable techniques for effectively applying some of the physically important operators and their kernel fast and with ease.
Two of the most important operators that we illustrate in this manual are the Poisson operator, and the Helmholtz operator (also note that heat/diffusion equation kernel is just a single Gaussian).
Herein, we discuss techniques for "thinking in MADNESS", which will allow the best utilization of the numerical tools underlying MADNESS (in most cases).
- Solve the integral equation
In many situations the integral operator associated with the differential operator has an analytic kernel. The simplest examples are convolution operators.
- The free-space Poisson equation is converted to a convolution with the Poisson (or Coulomb) kernel,
where![\[
\nabla^{2} u = -4\pi\rho \to u=G \ast \rho,
\]](form_22.png)
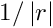
- The Schrödinger equation with potential
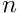
where![\[
- \frac{1}{2} \nabla^{2} \psi + V\psi = E \psi \to \psi = -2G \ast V\psi,
\]](form_25.png)
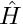
- Duhamel's principle can be appled to write a time-dependent differential equation with linear operator
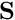
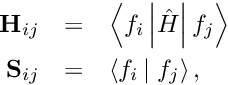
![\[
\hat{L}u + N(u,t) = \dot{u} \to u(t) = e^{\hat{L} t} u(0) + \int _{0}^{t} e^{\hat{L} (t-t')} N(u,t') \mathit{d}t'.
\]](form_29.png)
Most codes, including MADNESS, are bad at solving differential equations to high accuracy – this is why there is so much emphasis placed on finding a good preconditioner. The problem arises from the spectrum of the differential operator. Consider the Laplacian in 1D acting on a plane wave,
![\[
\frac{d^{2}}{\mathit{dx}^{2}}e^{i\omega x}=-\omega ^{2}e^{i\omega x}.
\]](form_30.png)
The Laplacian greatly amplify high frequencies 
The integral form is potentially better in many ways – accuracy, speed, robustness, asymptotic behavior, etc. If you really, really, want to solve the differential form, then instead of using the phrase "integral form" say "perfectly preconditioned differential form" so that you can do the right thing.
- Carefully analyze discontinuities, noise, singularities, and asymptotic forms
Your function needs to be evaluated at close to machine precision. The higher the order of the basis ( 
Discontinuities and singularities need to be consciously managed. Integrable point singularities might sometimes work unmodified (e.g., 
![\[
\exp(-r) \to \exp (-\sqrt{r^{2}+\sigma ^{2}}),
\]](form_33.png)
or replace a step function with
![\[
\theta(x) \to \theta(x, \lambda) = \frac{1}{2} (1 + \tanh\frac{x}{\lambda}),
\]](form_34.png)
or the Coulomb potential in 3-D with
![\[
\frac{1}{r} \to u(r,c) = \frac{1}{r} \mathrm{erf} \frac{r}{c} + \frac{1}{c\sqrt{\pi}} e^{-\left( \frac{r}{c} \right)^{2}}
\]](form_35.png)
subject to
![\[
\int_{0}^{\infty} \left(u(r, c) - r^{-1}\right) r^{2} d\mathit{r} = 0.
\]](form_36.png)
The integral indicates that the mean error is zero, independent of 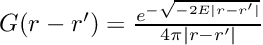
Numerical noise can be a problem if your function is evaluated using interpolation or some other approximation scheme, or when switching between representations (e.g., between forms suitable for small or large arguments). If you are observing inefficient projection into the basis, ensure that your approximation is everywhere smooth to circa 1 part in 
MADNESS itself computes to a finite precision, and when computing a point-wise function of a function (i.e., 
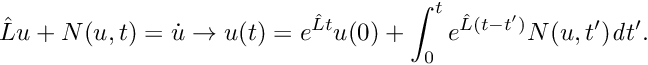
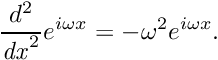
![\[
V(\rho(x)) = \frac{C}{\rho^{1/3}(x)},
\]](form_42.png)
where in the original problem one knows that 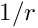
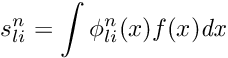
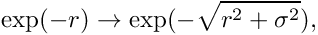
The function 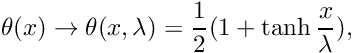
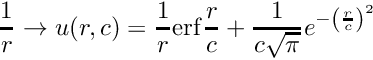
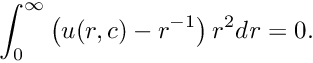
Some computations are intrinsically expensive. For instance, the function 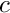
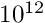
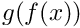
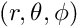
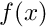
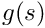
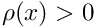
Choice of polynomial order ( 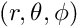
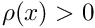
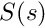
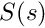
moldft we use the heuristic that to get an accuracy of 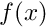
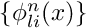
Previous: Load and memory balancing; Next: MADNESS environment variables