The source is here.
- Points of interest
- convolution with the Green's function/free-particle propagator
- use free-particle propagators construct different schemes to find the solution
- collocation methods on quadrature points
- Background
- This illustrates solution of a time-dependent Schrödinger equation.
We solve the following PDE
![\[
-\nabla^2 \psi(x,t) + V(x,t) \psi(x,t) = i\psi_t(x,t)
\]](form_244.png)
where the potential is
![\[
V(x,t) = -8 \exp((x - v \cdot t)^2)
\]](form_245.png)
and the velocity 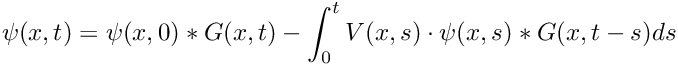
- Implementation
Splitting based schemes, such as Trotter and Chin-Chen, can be found in existing literatures.
The quadrature collocation method is based on the semi-group form of the equation
![\[
\psi(x,t) = \psi(x,0) * G(x,t) - \int_0^t V(x,s) \cdot \psi(x,s) * G(x,t-s) ds
\]](form_247.png)
where 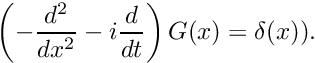
![\[
\left( - \frac{d^2}{dx^2} - i \frac{d}{dt} \right) G(x) = \delta(x)).
\]](form_249.png)
To find 
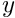
![$ [0,t] $](form_251.png)
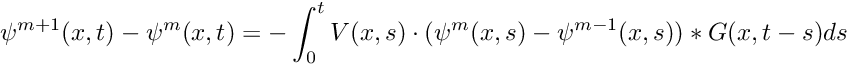
![$ [0,t] $](form_251.png)
The fixed-point iteration is applied to the correction term of the semi-group formulation,
![\[
\psi^{m+1}(x,t) - \psi^{m}(x,t) = - \int_0^t V(x,s) \cdot ( \psi^{m}(x,s) - \psi^{m-1}(x,s)) * G(x,t-s) ds
\]](form_253.png)
or
![\[
\delta^{m+1}(x,t) = - \int_0^t V(x,s) \cdot \delta^{m}(x,s) * G(x,t-s) ds
\]](form_254.png)
where 
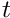
A much more efficient scheme would involve use of a non-linear equation solver instead of simple iteration.
Once we have the solutions at the 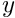
![$ [0,t] $](form_251.png)
- Reference
- Preprint.