The source is here.

Points of interest

Convolution with the negative energy (bound state) Helmholtz Green's function
Iterative solution of the integral form of the equation
Smooth truncation of the density to manage numerical noise amplified by nearly singular potential
Plotting of the solution and potential

Background

This illustrates solution of a non-linear Schrödinger motivated by exploring problems associated with equations of the same form from nuclear physics.

We seek the lowest eigenfunction of

$-\nabla^2 \psi(x) + V(x) \psi(x) = E \psi(x)$

where the potential is

$V(x) = -a \exp(-b x^2) + \frac{c}{(n(x)+\eta)^{1/3}} - d n(x)^{5/3} + V_{\mbox{shift}}$

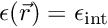
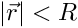
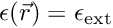
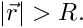
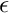
The parameters , , , , and $V_{\mbox{shift}}$ are given in the code. The density is given by

$n(x) = \psi(x)^2$

There would normally be multiple states occupied but for simplicity we are employing just one.

The first term in the potential is weak and seems to be there to stabilize the solution. The second term seems to act as a confining potential since it becomes large and positive when the density is small. The third term represents short-range attraction between particles, and the fourth adjusts the zero of energy.

[These notes were written by a chemist ... if you are a nuclear physicist could you please clean them up?].

Implementation

The integral form of the equation is

$\psi = - 2 G_{\mu} * \left ( V \psi \right)$

where $G_{\mu}$ is the Green's function for the Helmholtz equation

$\left( - \frac{d^2}{dx^2} + \mu^2 \right) G(x,x^{\prime}) = \delta(x-x^{\prime})$

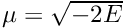
where $\mu = \sqrt{-2 E}$ .

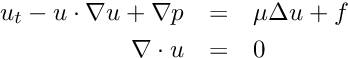
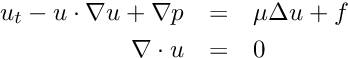
We employ a simple fixed-point iteration to the self-consistent solution, but strong damping or step restriction is necessary to ensure convergence. This is due to the nearly singluar potential, the problem being exacerbated by small $\eta$ . A reliable solution scheme seems to be to first solve with a large value of $\eta$ and then to reduce it in several steps to its final value. A much more efficient scheme would involve use of a non-linear equation solver instead of simple iteration.

The density is analytically everywhere positive, but numeric noise can introduce regions where it is zero or even slightly negative. To avoid very non-physical results, we smoothly switch values less than some threshold to a minimum value. This is preferable to employing a sharp cutoff.