The source is here.

Points of interest

use of iterative equation solver
convolution with the Green's function
unary operator to compute reciprocal of a function
use of diffuse domain approximation to represent interior surfaces
line and volume plots

Background

We wish to solve Poisson's equation within a non-homogeneous medium, i.e., in which the permittivity is not constant.

$\nabla . \left( \epsilon(r) \nabla u(r) \right) = - 4 \pi \rho(r)$

Expanding and rearranging yields,

$\nabla^2 u(r) = - \frac{1}{\epsilon(r)} \left( 4 \pi \rho(r) + \nabla \epsilon(r) . \nabla u(r) \right)$

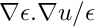
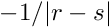
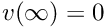
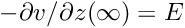
We can interpret $\rho / \epsilon$ as the effective free charge density and $\nabla \epsilon . \nabla u / \epsilon$ as the induced surface charge density. Assuming free-space boundary conditions at long range we can invert the Laplacian by convolution with the free-space Green's function that is $-1 / 4 \pi |r-s|$ . Note that MADNESS provides convolution with $G(r,s) = 1/|r-s|$ so you have to keep track of the $-1/4\pi$ yourself.

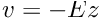
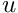
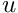
Thus, our equation becomes (deliberately written in the form of a fixed point iteration — given a guess for $u$ we can compute the r.h.s. and directly obtain a new value for $u$ that hopefully is closer to the solution)

$u = G * \left(\rho_{\mbox{vol}} + \rho_{\mbox{surf}} \right)$

where

$\rho_{\mbox{vol}} = \frac{\rho}{\epsilon}$

and

$\rho_{\mbox{surf}} = \frac{\nabla \epsilon . \nabla u}{4 \pi \epsilon}$

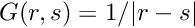
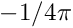
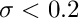
Let's solve a problem to which we know the exact answer — a point charge at the center of a sphere $R=2$ . Inside the sphere the permittivity is $\epsilon_1 = 1$ and outside it is $\epsilon_2 = 10$ . The exact solution is

$u(r) = \left \lbrace \begin{array}{cc} \frac{1}{\epsilon_2 |r|} & |r| > R \\ \frac{1}{\epsilon_1 |r|} + \left( \frac{1}{\epsilon_2} - \frac{1}{\epsilon_1} \right) \frac{1}{R} & |r| < R \end{array} \right .$

The surface charge density integrated over the suface has the value

$q_{\mbox{surface}} = -\frac{\epsilon_2 - \epsilon_1}{\epsilon_2} = -0.9$

To implement the problem in MADNESS we want the permittivity defined as a function over all space, so we define a characteristic function 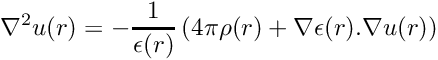$C(r)$ (or mask) that is defined to be one inside the sphere and zero outside

$C(r) = H(R-|r|)$

where $H(x)$ is the Heaviside step function. Hence, we have

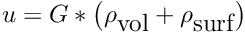
$\epsilon(r) = \epsilon_1 C(r) + \epsilon_2 \left( 1 - C(r) \right)$

To smooth the discontinuity we replace the Heaviside step function with

$H(x,\sigma) = \frac{1}{2} \left( 1 + \mathop{\mathrm{erf}} \frac{x}{\sigma} \right)$

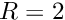
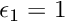
where $\sigma$ is the effective width of the step (0.2 in the code). Similarly, the point charge is replaced by a suitably normalized Gaussian with a an exponent sufficiently large as to appear as a point charge (delta function) on the scale of interest (we pick $\xi=100$ )

$\rho(r) = \left(\pi \xi \right)^{-3/2} e^{-\xi |r|^2}$

Starting from an initial guess we could try to iterate our equation for 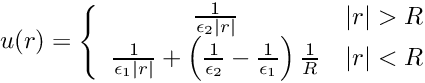$u(r)$ but, sadly, this does not converge reliably. The simplest approach is to introduce some damping or step restriction. With $m$ indicating the iteration number, we write

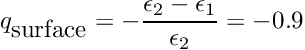
$u^{(m+1)} = \alpha u^{(m)} + (1-\alpha) G * \left(\rho^{(m)}_{\mbox{vol}} + \rho^{(m)}_{\mbox{surf}} \right)$

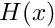
with $\alpha \in [0,1]$ . This works (for sufficiently small $\alpha$ ) and is implemented in the code.

A more robust approach is to use a solver that exploits information from previous iterations (the Krylov subspace) to estimate the optimal direction and length of the step to take. Such a solver is provided by nonlinsol.h. Each iteration we pass the current solution and corresponding residual to the solver and it provides the next trial vector.

In the code you can switch between using the solver or simple iteration by changing the value of USE_SOLVER .

One final point is how to compute the reciprocal of the permittivity. This operation is not provided explicity by MADNESS, in part because even functions that are analytically never zero, might be (nearly) zero due to numerical truncation. Handling this issue correctly is problem specific. More generally, we want to compute a function-of-a-function. If 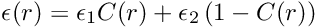$f(r)$ is a MADNESS function that takes a d-dimensional vector as its argument (in this examaple $d=3$ ) and $F(x)$ is computable function that takes a scalar argument, we want to compute the new MADNESS function

$g(r) = F(f(r))$

There are various ways to do this. The simplest is employed here — we define a function (reciprocal() ) that is passed into the unaryop() method that modifies the function in-place. This simple approach is justified here since we know our input function is never zero even due to numerical noise, and the output function is about as smooth as the input. If it were not, we might have to refine the input function to obtain the desired precision.