The source is here.

Points of interest

convolution with the Green's function
need to adjust the zero of energy to use the bound-state Green's function
failure of simple fixed-point iteration
use of simple non-linear equation solver
plotting 3D function along a line

Background

We seek the ground state of the 3D Schrodinger equation

$\left( -\frac{1}{2} \nabla^2 + V(r) \right) \psi(r) = E \psi(r)$

with

$V(r) = \frac{1}{2} |r|^2$

As usual, we rewrite the differential equation into integral form

$\psi(r) = \left( -\frac{1}{2} \nabla^2 - E \right)^{-1} V(r) \psi(r)$

but unfortunately we are left with two problems.

First, recall that application of the inverse of the differential operator corresponds to convolution with the Green's function to the Helmholtz equation that satisfies

$\left(-\nabla^2 + \mu^2 \right) G(r,r'; \mu) = \delta(r-r')$

In 3D, we have

$G(r,r'; \mu) = \frac{e^{-\mu |r-r'|}}{4 \pi |r-r|}$

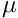
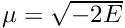
that MADNESS can currently only apply efficiently for real $\mu$ and since $\mu = \sqrt{-2 E}$ only for negative energies (hence bound states). But for the harmonic oscillator there are no free particle states and the zero of energy is not chosen to describe the lowest energy of a free particle but simply as the zero of potential energy. To solve this problem we can shift the zero of energy down by subtracting a constant ( $\Delta$ ) from both sides of the equation, hence making the effective ground state energy negative.

$\psi(r) = \left( -\frac{1}{2} \nabla^2 - E + \Delta \right)^{-1} \left( V(r) -\Delta\right) \psi(r)$

How negative do we need to make the energy? To answer this we need to discuss the second problem. The fixed-point iteration described by the integral equation only reliably converges to the ground state if the potential is negative everywhere the wave function is significant. The exact solution is 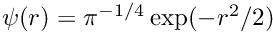$\psi(r)=\pi^{-1/4}\exp(-r^2 / 2)$ (with $E=$1.5) that becomes 1e-6 (but how small is small enough?) at where is 14.0. So let's take this as the value of $\Delta$ and try the fixed point iteration. Bad news. It starts converging (slowly) to the right answer but then diverges and even damping (step restriction) does not solve the problem. We have to make the shift large enough to make the potential negative in the entire volume to avoid the divergence, but this makes the convergence really slow.

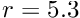
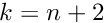
The fix is to not rely upon the simple fixed point iteration but to use an equation solver to force convergence. This also enables us to choose the size of the shift to optimize the rate of convergence (empirically 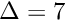$\Delta=7$ is best) rather than being forced to pick a large value. We use the very easy to use solver in mra/nonlinsol.h .

[Aside. It is possible to apply the operator for positive energies, but efficient application requires separate treatment of the singular and the long-range oscillatory terms, and the latter is presently not a production capability of MADNESS. If you need this, let us know.]